Pyhton: NumPy Matrix dan Aljabar Linear: Difference between revisions
| (4 intermediate revisions by the same user not shown) | |||
| Line 36: | Line 36: | ||
A | A | ||
matrix([[1., 2.], | |||
matrix([[ 1., | [3., 4.], | ||
[ 3., | [5., 6.]]) | ||
[ 5., | |||
Kami juga dapat menggunakan gaya Matlab dengan memberikan string bukan list: | Kami juga dapat menggunakan gaya Matlab dengan memberikan string bukan list: | ||
| Line 46: | Line 45: | ||
B = np.matrix("1.,2; 3,4; 5,6") | B = np.matrix("1.,2; 3,4; 5,6") | ||
B | B | ||
matrix([[1., 2.], | |||
[3., 4.], | |||
[5., 6.]]) | |||
==Vector sebagai matrix== | |||
Vektor ditangani sebagai matriks dengan satu baris atau satu kolom: | |||
x = np.matrix("10., 20.") | |||
x | |||
matrix([[10., 20.]]) | |||
x.T | |||
matrix([[10.], | |||
[20.]]) | |||
Berikut adalah contoh perkalian matriks dan vektor: | |||
x = np.matrix("4.;5.") | |||
x | |||
matrix([[4.], | |||
[5.]]) | |||
matrix([[ 4.], | |||
[ 5.]]) | |||
A = np.matrix([[1.,2], [3,4], [5,6]]) | |||
A | |||
matrix([[ 1., | |||
[ 3., | matrix([[1., 2.], | ||
[ 5., | [3., 4.], | ||
[5., 6.]]) | |||
A*x | |||
matrix([[14.], | |||
[32.], | |||
[50.]]) | |||
Untuk vektor, pengindeksan memerlukan dua indeks: | |||
print( x[0,0], x[1,0] ) | |||
4.0 5.0 | |||
Catatan | |||
Meskipun np.matrix mengambil bentuk matriks nyata dan terlihat bagus, biasanya, untuk sebagian besar kasus, array sudah cukup baik. | |||
==Rank== | |||
import numpy as np | |||
A = np.ones((4,3)) | |||
A | |||
array([[ 1., 1., 1.], | array([[ 1., 1., 1.], | ||
[ 1., 1., 1.], | [ 1., 1., 1.], | ||
[ 1., 1., 1.], | [ 1., 1., 1.], | ||
[ 1., 1., 1.]]) | [ 1., 1., 1.]]) | ||
# np.rank(A) # rank sudah sudah tidak ada NumPy | |||
# 2 | |||
Perhatikan bahwa pangkat array bukanlah pangkat matriks dalam aljabar linier (dimensi ruang kolom) tetapi jumlah subskrip yang diperlukan! | |||
Skalar memiliki rank 0: | |||
x = np.array(10) | |||
x | |||
array(10) | array(10) | ||
# np.rank(x) # rank sudah sudah tidak ada NumPy | |||
# 0 | |||
Menghitung rank matrix | |||
from numpy.linalg import matrix_rank | |||
matrix_rank(np.eye(4)) # Full rank matrix | |||
4 | |||
I=np.eye(4); I[-1,-1] = 0. # rank deficient matrix | |||
matrix_rank(I) | |||
3 | |||
matrix_rank(np.ones((4,))) # 1 dimension - rank 1 unless all 0 | |||
1 | |||
matrix_rank(np.zeros((4,))) | |||
0 | 0 | ||
NumPy mendukung array dari dimensi apa pun seperti peringkat 3 (2x2x2): | |||
array([[[ 1., | |||
A = np.ones((2,2,2)) | |||
A | |||
array([[[1., 1.], | |||
[1., 1.]], | |||
[[ 1., | [[1., 1.], | ||
[ 1., | [1., 1.]]]) | ||
A[1,0,1] | |||
1.0 | |||
dot product | dot product | ||
A = np.array([[1,2],[3,4]]) | |||
A | |||
array([[1, 2], | array([[1, 2], | ||
[3, 4]]) | [3, 4]]) | ||
b = np.array([10, 20]) | |||
b | |||
array([10, 20]) | array([10, 20]) | ||
ans = np.dot(A,b) | |||
ans | |||
array([ 50, 110]) | array([ 50, 110]) | ||
| Line 152: | Line 185: | ||
Ax = b : numpy.linalg | |||
Kita akan solve Ax = b: | |||
import numpy as np | |||
from numpy.linalg import solve | |||
A = np.array([[1,2],[3,4]]) | |||
A | |||
array([[1, 2], | array([[1, 2], | ||
[3, 4]]) | [3, 4]]) | ||
b = np.array([10, 20]) | |||
b | |||
array([10, 20]) | |||
x = solve(A,b) | |||
x | |||
array([0., 5.]) | |||
==Eigen Value dan Vector== | ==Eigen Value dan Vector== | ||
import numpy as np | |||
from numpy.linalg import eig | |||
A = np.array([[1,2],[3,4]]) | |||
eig(A) | |||
(array([-0.37228132, 5.37228132]), | |||
array([[-0.82456484, -0.41597356], | |||
[ 0.56576746, -0.90937671]])) | |||
Eig mengembalikan dua tupel: yang pertama adalah nilai eigen dan yang kedua adalah matriks yang kolomnya berupa dua vektor eigen. | |||
Kami dapat membongkar tupel: | |||
eigen_val, eigen_vec = eig(A) | |||
eigen_val | |||
array([-0.37228132, 5.37228132]) | |||
eigen_vec | |||
array([[-0.82456484, -0.41597356], | |||
[ 0.56576746, -0.90937671]]) | |||
==Quadrature== | |||
Kita ingin menghitung ∫03 x^4 dx=2434: | |||
from scipy.integrate import quad | |||
def f(x): return x**4 | |||
quad(f, 0., 3.) | |||
(48.599999999999994, 5.39568389967826e-13) | (48.599999999999994, 5.39568389967826e-13) | ||
Tuple yang dikembalikan menunjukkan (ans, error estimate). | |||
Kita bisa mendapatkan jawaban yang sama jika kita menggunakan lambda sebagai gantinya: | |||
quad(lambda x: x**4, 0, 3) | |||
(48.599999999999994, 5.39568389967826e-13) | |||
==Referensi== | ==Referensi== | ||
* http://www.bogotobogo.com/python/python_numpy_matrix_tutorial.php | * http://www.bogotobogo.com/python/python_numpy_matrix_tutorial.php | ||
Latest revision as of 00:27, 8 April 2023
Sumber: http://www.bogotobogo.com/python/python_numpy_matrix_tutorial.php
Apa beda antara numpy dot() and inner()
Mari kita lihat ke 2D array:
import numpy as np a=np.array([[1,2],[3,4]]) b=np.array([[11,12],[13,14]])
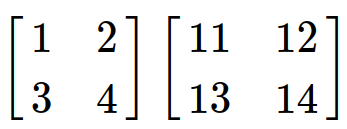
np.dot(a,b)
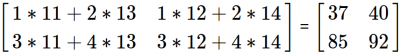
array([[37, 40],
[85, 92]])
np.inner(a,b)
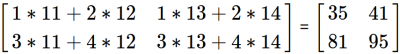
array([[35, 41],
[81, 95]])
NumPy Matrix
Bab-bab tentang NumPy telah menggunakan array (NumPy Array Basics A dan NumPy Array Basics B). Namun, untuk area tertentu seperti aljabar linier, kita mungkin ingin menggunakan matriks.
import numpy as np A = np.matrix([[1.,2], [3,4], [5,6]]) A
matrix([[1., 2.],
[3., 4.],
[5., 6.]])
Kami juga dapat menggunakan gaya Matlab dengan memberikan string bukan list:
import numpy as np
B = np.matrix("1.,2; 3,4; 5,6")
B
matrix([[1., 2.],
[3., 4.],
[5., 6.]])
Vector sebagai matrix
Vektor ditangani sebagai matriks dengan satu baris atau satu kolom:
x = np.matrix("10., 20.")
x
matrix(10., 20.)
x.T
matrix([[10.],
[20.]])
Berikut adalah contoh perkalian matriks dan vektor:
x = np.matrix("4.;5.")
x
matrix([[4.],
[5.]])
A = np.matrix([[1.,2], [3,4], [5,6]])
A
matrix([[1., 2.],
[3., 4.],
[5., 6.]])
A*x
matrix([[14.],
[32.],
[50.]])
Untuk vektor, pengindeksan memerlukan dua indeks:
print( x[0,0], x[1,0] )
4.0 5.0
Catatan
Meskipun np.matrix mengambil bentuk matriks nyata dan terlihat bagus, biasanya, untuk sebagian besar kasus, array sudah cukup baik.
Rank
import numpy as np A = np.ones((4,3)) A
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])
# np.rank(A) # rank sudah sudah tidak ada NumPy # 2
Perhatikan bahwa pangkat array bukanlah pangkat matriks dalam aljabar linier (dimensi ruang kolom) tetapi jumlah subskrip yang diperlukan!
Skalar memiliki rank 0:
x = np.array(10) x
array(10)
# np.rank(x) # rank sudah sudah tidak ada NumPy # 0
Menghitung rank matrix
from numpy.linalg import matrix_rank matrix_rank(np.eye(4)) # Full rank matrix
4
I=np.eye(4); I[-1,-1] = 0. # rank deficient matrix matrix_rank(I)
3
matrix_rank(np.ones((4,))) # 1 dimension - rank 1 unless all 0
1
matrix_rank(np.zeros((4,)))
0
NumPy mendukung array dari dimensi apa pun seperti peringkat 3 (2x2x2):
A = np.ones((2,2,2)) A
array([[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]])
A[1,0,1]
1.0
dot product
A = np.array([[1,2],[3,4]]) A
array([[1, 2],
[3, 4]])
b = np.array([10, 20]) b
array([10, 20])
ans = np.dot(A,b) ans
array([ 50, 110])
Ax = b : numpy.linalg
Kita akan solve Ax = b:
import numpy as np from numpy.linalg import solve A = np.array([[1,2],[3,4]]) A
array([[1, 2],
[3, 4]])
b = np.array([10, 20]) b
array([10, 20])
x = solve(A,b) x
array([0., 5.])
Eigen Value dan Vector
import numpy as np from numpy.linalg import eig A = np.array([[1,2],[3,4]]) eig(A)
(array([-0.37228132, 5.37228132]),
array([[-0.82456484, -0.41597356],
[ 0.56576746, -0.90937671]]))
Eig mengembalikan dua tupel: yang pertama adalah nilai eigen dan yang kedua adalah matriks yang kolomnya berupa dua vektor eigen.
Kami dapat membongkar tupel:
eigen_val, eigen_vec = eig(A) eigen_val
array([-0.37228132, 5.37228132])
eigen_vec
array([[-0.82456484, -0.41597356],
[ 0.56576746, -0.90937671]])
Quadrature
Kita ingin menghitung ∫03 x^4 dx=2434:
from scipy.integrate import quad def f(x): return x**4 quad(f, 0., 3.)
(48.599999999999994, 5.39568389967826e-13)
Tuple yang dikembalikan menunjukkan (ans, error estimate).
Kita bisa mendapatkan jawaban yang sama jika kita menggunakan lambda sebagai gantinya:
quad(lambda x: x**4, 0, 3)
(48.599999999999994, 5.39568389967826e-13)