Orange: Manifold Learning: Difference between revisions
Onnowpurbo (talk | contribs) No edit summary |
Onnowpurbo (talk | contribs) No edit summary |
||
| Line 5: | Line 5: | ||
Nonlinear dimensionality reduction. | Nonlinear dimensionality reduction. | ||
==Input== | |||
Data: input dataset | |||
==Output== | |||
Transformed Data: dataset with reduced coordinates | |||
Manifold Learning is a technique which finds a non-linear manifold within the higher-dimensional space. The widget then outputs new coordinates which correspond to a two-dimensional space. Such data can be later visualized with Scatter Plot or other visualization widgets. | Manifold Learning is a technique which finds a non-linear manifold within the higher-dimensional space. The widget then outputs new coordinates which correspond to a two-dimensional space. Such data can be later visualized with Scatter Plot or other visualization widgets. | ||
| Line 18: | Line 18: | ||
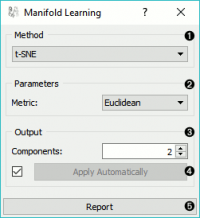
* Method for manifold learning: | |||
** t-SNE | |||
** MDS, see also MDS widget | |||
** Isomap | |||
** Locally Linear Embedding | |||
** Spectral Embedding | |||
* Set parameters for the method: | |||
** t-SNE (distance measures): | |||
*** Euclidean distance | |||
*** Manhattan | |||
*** Chebyshev | |||
*** Jaccard | |||
*** Mahalanobis | |||
*** Cosine | |||
** MDS (iterations and initialization): | |||
*** max iterations: maximum number of optimization interactions | |||
*** initialization: method for initialization of the algorithm (PCA or random) | |||
** Isomap: | |||
*** number of neighbors | |||
** Locally Linear Embedding: | |||
*** method: | |||
**** standard | |||
**** modified | |||
**** hessian eigenmap | |||
**** local | |||
*** number of neighbors | |||
*** max iterations | |||
** Spectral Embedding: | |||
*** affinity: | |||
**** nearest neighbors | |||
**** RFB kernel | |||
* Output: the number of reduced features (components). | |||
* If Apply automatically is ticked, changes will be propagated automatically. Alternatively, click Apply. | |||
* Produce a report. | |||
Manifold Learning widget produces different embeddings for high-dimensional data. | Manifold Learning widget produces different embeddings for high-dimensional data. | ||
Revision as of 01:54, 29 January 2020
Sumber: https://docs.biolab.si//3/visual-programming/widgets/unsupervised/manifoldlearning.html
Nonlinear dimensionality reduction.
Input
Data: input dataset
Output
Transformed Data: dataset with reduced coordinates
Manifold Learning is a technique which finds a non-linear manifold within the higher-dimensional space. The widget then outputs new coordinates which correspond to a two-dimensional space. Such data can be later visualized with Scatter Plot or other visualization widgets.
- Method for manifold learning:
- t-SNE
- MDS, see also MDS widget
- Isomap
- Locally Linear Embedding
- Spectral Embedding
- Set parameters for the method:
- t-SNE (distance measures):
- Euclidean distance
- Manhattan
- Chebyshev
- Jaccard
- Mahalanobis
- Cosine
- MDS (iterations and initialization):
- max iterations: maximum number of optimization interactions
- initialization: method for initialization of the algorithm (PCA or random)
- Isomap:
- number of neighbors
- Locally Linear Embedding:
- method:
- standard
- modified
- hessian eigenmap
- local
- number of neighbors
- max iterations
- method:
- Spectral Embedding:
- affinity:
- nearest neighbors
- RFB kernel
- affinity:
- t-SNE (distance measures):
- Output: the number of reduced features (components).
- If Apply automatically is ticked, changes will be propagated automatically. Alternatively, click Apply.
- Produce a report.
Manifold Learning widget produces different embeddings for high-dimensional data.

From left to right, top to bottom: t-SNE, MDS, Isomap, Locally Linear Embedding and Spectral Embedding.
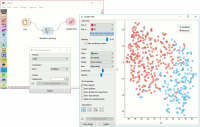
Contoh
Manifold Learning widget transforms high-dimensional data into a lower dimensional approximation. This makes it great for visualizing datasets with many features. We used voting.tab to map 16-dimensional data onto a 2D graph. Then we used Scatter Plot to plot the embeddings.